OvR 与 OvO - 逻辑回归解决多分类问题
所有的二分类算法都可以通过以下的方法改造成多分类算法:
-
OvR (One vs Rest) 也叫 (One vs All) 每次只做二分类,区分这个新来的样本点在一个类别和其他的类别中的预测值,然后对其他类别也做这样的分类,得到在每个分类上的预测值,取最大的值对应的类别为这个新来样本点的类别。
n个类别就要n个分类, 处理一个分类要T, 则要N*T的复杂度 -
OvO (One vs One) 每次只挑出2个类别进行二分类, 如果总共有4个类别,则可以形成 $C_4^2 = 6$ 对这样的分类。 复杂度: $C_n^2 * T$. 因为每次都只用2个类别比较,没有混淆其他类别的信息,所有分类会更加准确。
sklearn 中的Logistic Regression默认支持多分类,用超参数为 multi_class = 'ovr' or 'ovo'
我这个版本sklearn默认使用 multiclass='ovo', solver='newton-cg' 方式, 既ovo mode. 可以通过使用multiclass='ovr', solver='liblinear'改成ovr mode.
鸢尾花测试数据用2维样本特征做3分类:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[:, :2]#为了可视化,这里只取iris里的前2个维度作为特征进行fit
y = y[:] #分类3中鸢尾花,不再是二分类问题,而是多分类问题了
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1] - axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3] - axis[2])*100)).reshape(-1, 1)
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A', '#FFF59D', '#90CAF9'])
plt.contourf(x0, x1, zz, cmap=custom_cmap)
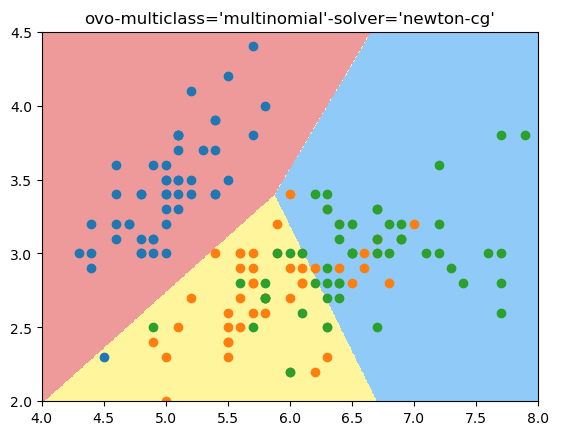
ovo 多分类模式:
log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)
plot_decision_boundary(log_reg, [4, 8, 2, 4.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.scatter(X[y==2, 0], X[y==2, 1])
结果:
score: 0.7894736842105263
ovr模式:
log_reg1 = LogisticRegression(multi_class='ovr', solver='liblinear') # 这个方式是ovr的方式
log_reg1.fit(X_train, y_train)
log_reg1.score(X_test, y_test)
plot_decision_boundary(log_reg1, [4, 8, 2, 4.5])
plt.scatter(X[y==0, 0], X[y==0, 1])
plt.scatter(X[y==1, 0], X[y==1, 1])
plt.scatter(X[y==2, 0], X[y==2, 1])
plt.title("ovr-multiclass='ovr'-solver='liblinear'")
结果:
score: 0.6578947368421053
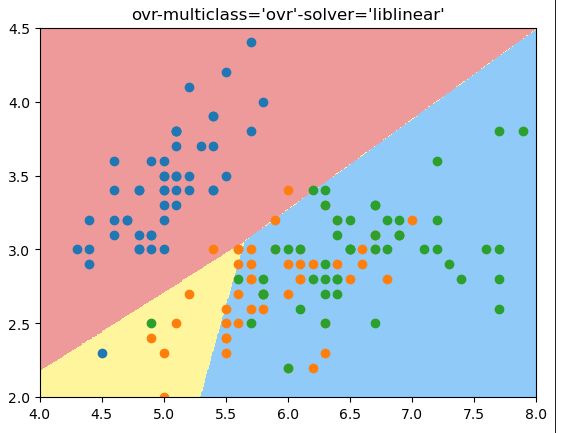
结论:可以看出来,ovr得到的准确度没有ovo好,从决策边界看,ovo的决策边界也更合理
OvO and OvR 分类器
sklearn提供了OvO and OvR 分类器,任何一个二分类算法都可以用这2个分类器实现多分类功能。
from sklearn.multiclass import OneVsRestClassifier
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
log_reg1 = LogisticRegression(multi_class='ovr', solver='liblinear')
ovr = OneVsRestClassifier(log_reg1)
ovr.fit(X_train, y_train)
ovr.score(X_test, y_test)
score: 0.9473684210526315
from sklearn.multiclass import OneVsOneClassifier
ovo = OneVsOneClassifier(log_reg)
ovo.fit(X_train, y_train)
ovo.score(X_test, y_test)
score: 1.0