模拟实现梯度下降法
import numpy as np
import matplotlib.pyplot as plt
plot_x = np.linspace(-1, 6, 141)
def dJ(theta):#求theta点对应的梯度
return 2*(theta - 2.5)
def J(theta):#损耗函数
try:
return (theta-2.5)**2 - 1
except:
return float('inf')
def gradient_descent(initial_theta, eta, n_iters=1e3, epsilon=1e-8):
theta = initial_theta
theta_history=[]
theta_history.append(initial_theta)
i_iter = 0
while (i_iter < n_iters):
last_theta = theta
gradient = dJ(theta)
theta = theta - eta*gradient
theta_history.append(theta)
if np.abs(J(theta) - J(last_theta)) < epsilon:
break
i_iter += 1
return theta_history
def plot_theta_history():
plt.plot(plot_x, J(plot_x))
plt.plot(np.array(theta_history), J(np.array(theta_history)), color='r', marker='+')
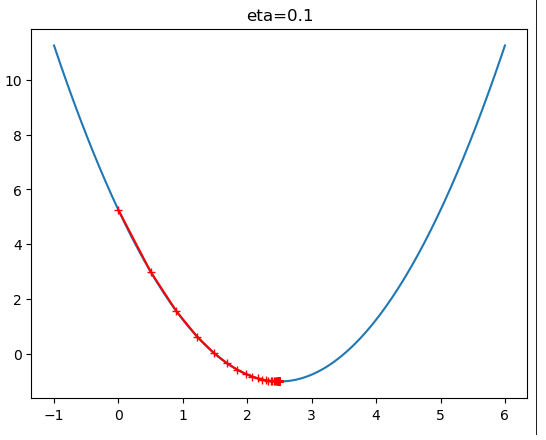
#plt.title("eta=0.1")
theta_history = gradient_descent(initial_theta=0, eta = 0.1, epsilon=1e-8)
plot_theta_history()
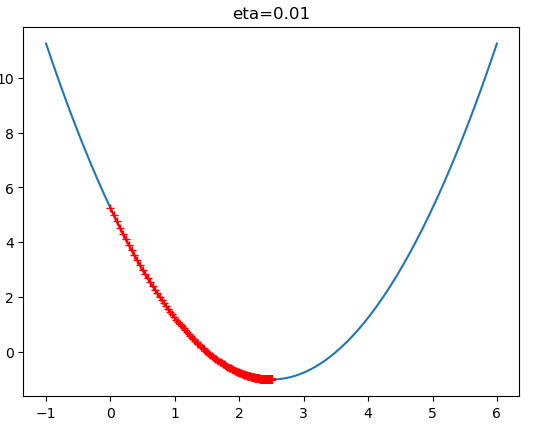
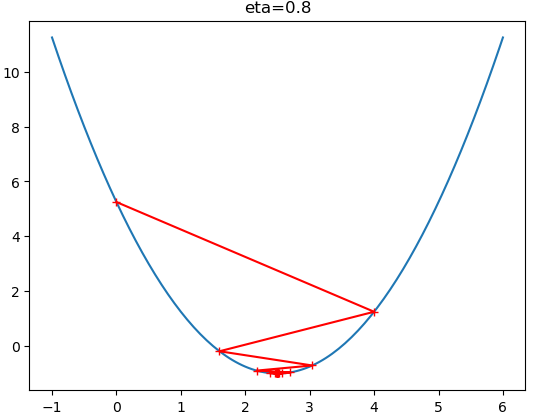
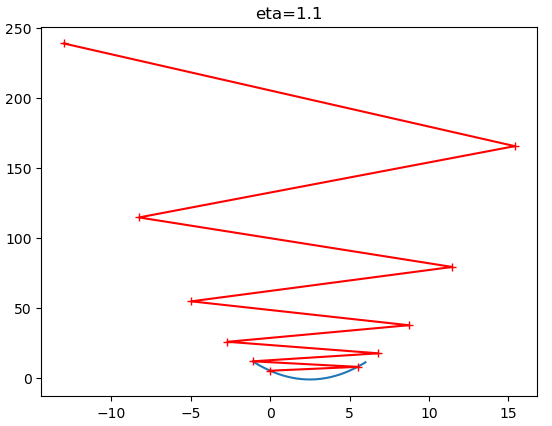
$\eta$ 值会影响算法能否快速收敛: