多元线性回归
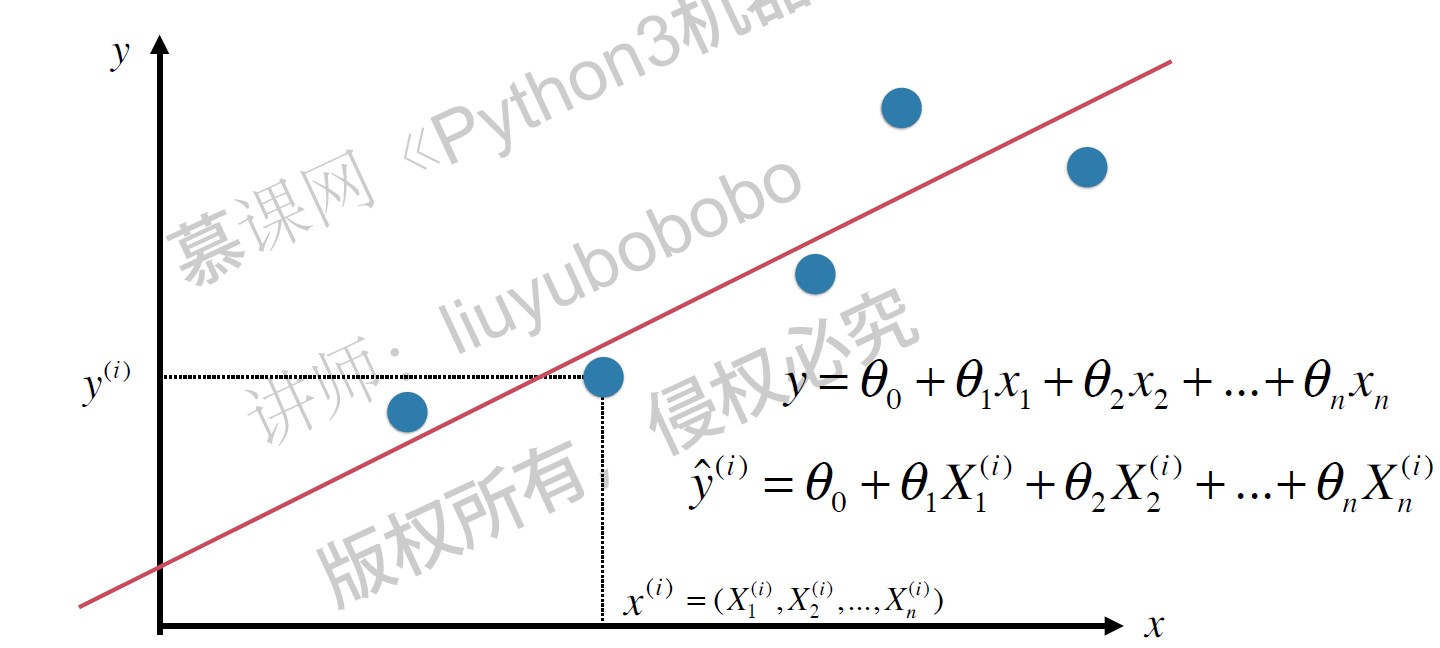


多元线性回归的目标函数: $$\hat y = X_b \cdot \theta $$ 使$ \sum_{i=1}^m(y^{(i)} - {\hat y}^{(i)})^2 $ 尽可能小。 即使 $ (y - X_b \cdot \theta)^T (y-X_b \cdot \theta)$ 尽可能小。
以下是多元线性回归的正规方程解( Normal Equation), 时间复杂度高: $O(n^3)$ (优化后是 $O(n^{2.4})$), 优点是不需要对数据做归一化处理。
$$ \theta = (X_b^TX_b)^{-1} X_b^T y $$
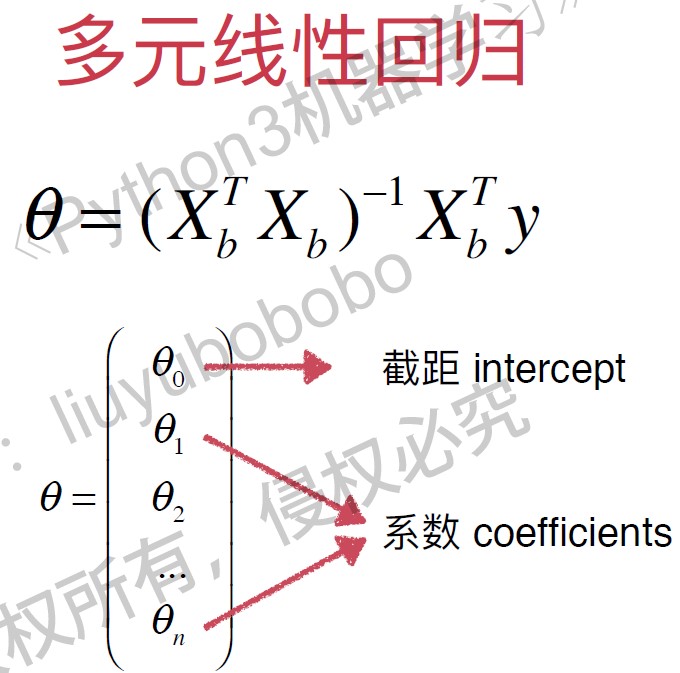
总结:
| kNN | Linear Regression |
|---|---|
| 非参数学习 | 典型的参数学习算法 |
| 既可以解决分类问题,又可以解决回归问题 | 虽然是很多分类算法的基础(Logistic Regression), 但是只能解决回归问题 |
| 对数据没有假设 | 对数据有线性的假设 |
| 对数据无解释性 | 对数据有强解释性 |